我一直在想能不能在屏幕上显示一个算出来的图像,经过近视眼模糊以后正好变得清楚。但一直没有机会静下心来把数学推完并且用代码实现。最近趁着休假把整个问题推完了。下面我们首先从数学的角度出发把整个问题的脉络理清楚,然后做一个模拟实验,看看我们的思路有什么问题(ringing),进而引入image prior的概念来解决这个问题。接下来用相机做一个实战实验,引入Point Spread Function的概念,从而在实际操作上演示这个问题可以怎么解决。
人眼的近视远视(等价于相机镜头的失焦),以及散光(等价于镜头的散光)都可以用一个简单的卷积操作来描述。只是近视远视是一个圆形的卷积核(从三维来看类似一个波峰),散光是一个方形的卷积核(从三维来看类似一个圆柱)。关于卷积,这里不具体介绍定义,感兴趣的同学可以自行查找。一个例子见下。对于这样的一个图像,和这样的一个矩阵(卷积核),他们卷积的结果就是把这个图象变模糊了:
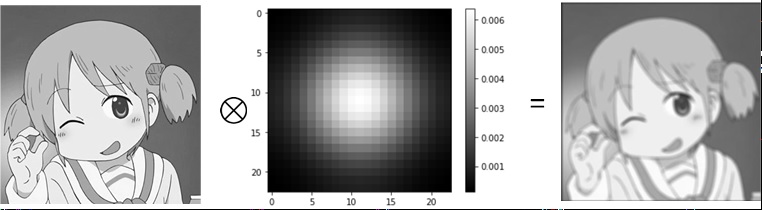
其中\(\bigotimes\)表示卷积操作。考虑到散光和近视本质上和远视是一样的,只是卷积核的具体形式不同,所以我们这里只考虑远视(失焦)的情况。为了分析简便,我们采用高斯模糊矩阵作为卷积核。于是我们的问题就变成了,给定一个矩阵(图像)\(I_0\),求一个矩阵\(I\),使得它和一个高斯模糊矩阵卷积的结果就是\(I_0\)。注意虽然这里\(I_0\)是一个矩阵,但这个算法可以非常简单地拓展到三通道的情况,把\(I_0\)换成一个张量即可。用数学的形式把这个问题写出来就是:
这里注意两个问题,一个是为什么外面的距离用\(L_2\) norm。答案是为了实现方便。其实\(L_2\)并不是最好的方案,如果最终这个要做成产品的话我很可能会换用其他的距离量度。另一个问题是,这个问题有解析解吗?如果我们考虑\(I \bigotimes K = I_0\)的话,会发现这个问题其实是under-constrained。由于卷积需要做padding,所以未知数的数量会大于实际约束条件的数量。所以这个问题只能用数值优化来做数值解。我自己撸了一个Adam,把上面的图片作为\(I_0\)扔进去,得到的图像如下:

这尼玛什么鬼。是不是我们的算法实现错了?我们用高斯模糊矩阵卷积一下,诶,结果却是对的:

这是为什么呢?原因很简单,我们并没有让优化算法把I做得"自然",而只让它卷积以后尽可能地接近输入的\(I_0\)。而这种像水波纹一样的图像可以得到一个非常接近\(I_0\)的结果,自然就收敛到上面去了。这种现象叫做ringing,是这种反卷积优化中常见的问题。解决方法也很简单,我们通过改动目标函数,告诉优化算法把\(I\)同时做得"自然"就好了。具体地说,我们在目标函数里面加入一个额外的正则项(regularizer,又叫image prior)即可。这里面还有贝叶斯角度的解释,各种prior设计的技巧,具体说来可能要说三天三夜,这里作为实验的第一个版本,我们先用图像差分的\(L_2\) norm:
这里\lambda是一个平衡两项的超参数。\bigtriangledown指的是图像的梯度,也就是每个像素和周围像素的差值。如果我们用这个新的目标函数做优化的话,得到的图像就好看多了:

这里可以用\(\lambda\)来平衡ringing的程度。\(\lambda\)越大,图像越自然,但卷积之后图像和\(I_0\)的距离则会受到一些影响。这里为了后面说明问题,把\(\lambda\)设得比较小。此时如果我们对这个图像直接做高斯模糊的话,得到的结果是这样的:

问题到这里看上去就解决了。我们已经得到了一个看起来比较正常的图像,这个图象在用高斯模糊模拟的失焦下可以还原输入的清晰的图像。如果对比输出和输入图像的话,你也许已经发现了,这好像和锐化有一些关系!如果我们输入一个经过高斯模糊的图像的话,其实可以用这种方法还原原来的图像。比如下面是一个例子。甚至我非常怀疑Photoshop的Smart Sharpening就是这么做的。

下面就是见证奇迹的时刻了。如果我们的推导是正确的话,我们用相机翻拍这个图像I,加上一些虚焦,应该可以得到原来的图像I_0。我们试试看:

但我发现不论怎么调整虚焦,出来的图像总是和原先清晰的图像离得很远。最好的情况就是上面这张图了。是我们的推导出了什么问题吗?这里就要牵涉到一些摄影方面的知识了。如果你用大光圈虚化拍摄一个点光源的话,出来的光斑其实不是一个理想的高斯模糊矩阵(除了一些极其特殊的双光圈STF镜头),而是一个圆。这个圆叫做镜头的Point Spread Function(PSF)。所以我们把卷积核改成了下面的形式:

经过这样的改动以后,得到的图像和虚焦翻拍的结果如下:

这下我们可以得到非常类似原图像的翻拍了!不过这张图效果还不是很明显。我们又试了另一个图像,这次降低\lambda把ringring调地更显著:

可以看到相机虚焦的确可以把ringing去掉,并且得到一个相对清晰的结果。不过可能是因为卷积核过大,最终地锐度和原始图像还是有一定差距,不够清晰。但基本上能实现原先的设计目标了,甚至可以让人摘掉眼镜,只看一些奇怪的过度锐化的图像就可以在视网膜上得到正常清晰的影像。另外,严谨地说镜头的PSF是需要精确测定的,同时视场内不同位置的PSF也不一样。所以如果想要进一步提升效果的话,还需要做更细致的工作。
其实这个技术的应用场景非常广。比如其实我们完全可以不同镜头拍照,而用一些经过特殊设计的小孔(如下图)拍照:

这种镜头的好处是像小孔一样没有像差,但光圈可以到f/2左右。我自己做了一个这样的相机,拍出来的照片类似这样:

你能实现上面说的算法,还原出原始的图像吗?
Comments