当城市灯火渐暗,夜空澄澈如洗,你或许会注意到几颗格外明亮的行星,仿佛约好般排成一线,在苍穹中彼此呼应。这就是传说中的行星连珠现象。虽然这些天体并没有真正在太空里严丝合缝地排成几何直线,但从地球的视角看,多颗行星似乎被一根看不见的线串联在一起,它们形成的视觉队列依然令人屏息。不论中外,从25年1月开始,诸多媒体都在热议所谓的六星或七星连珠现象。有人为之惊叹,也有人质疑其中的科学成分。那么如果我们想找出过去20年(或任意一段时间)里所有可能出现的n星连珠现象,该怎么做呢?
在现代天文学研究里,一种常见思路是用程序模拟行星位置并进行量化评估。行星的运动并非随机杂乱,而是依循各自的椭圆轨道绕太阳公转。虽然在夜空中它们的相对位置可能几天或几小时就发生些微变化,但只要我们掌握各自轨道参数、再结合地球上观测的具体条件,就能较精确地计算它们在不同时刻的坐标。好在这样的计算模拟并不需要我们手动进行,像Skyfield这样的天文计算库,既能提供高精度的行星历,也能便捷地将得到的太阳系坐标转换到地面观测者所在位置。
不过,行星连珠主要与行星绕太阳公转时的几何分布有关,地球自转的影响相对较小。为了方便分析,我们通常采用黄道坐标系来记录行星的位置,把黄道面当作基准。太阳在一年四季里看似在天球上缓缓移动,这条轨迹之所以被称为黄道,正是因为地球绕太阳公转,而我们又站在地球上向外看,所形成的投影现象。简单来说,地球绕太阳转的轨道平面就是黄道面,映射到天球上就成为黄道。这个“主干道”之所以重要,是因为大多数行星的运行平面都跟它相差不大,所以当我们把行星坐标转换到黄道坐标系时,能更准确地呈现它们绕日公转时的整体布局。
从数学上说,黄道坐标并不会改变行星之间的实际角度,但它能让我们更直观地看出这些行星是否挤在同一个经度范围里。在运行具体程序时,我们先在一个给定的时间区间内(比如2010到2030年),针对每一天或更细的时间步长,逐一计算出各行星在黄道坐标系中的经度和纬度。
然而,只掌握行星都在哪里还不足以直接判定它们是不是连珠。问题的核心在于,我们要给这个看似直观的整齐排布一个量化的定义。具体地说,我们要把“行星排得很整齐”这个直觉加以拆解:
首先,这些行星至少在晚上要能看见,不能跟着太阳朝升夕落。不要笑,考虑到绝大多数行星并不会偏离黄道太远,这其实是影响最大的一个因素。否则就算几何上再完美,如果这些行星中大多数都深藏在太阳的光辉之中,或根本不在地平线上可观测,视觉上便无从谈起连珠。因此,我们先利用北京的经纬度和时间,利用行星,太阳,和地平线的相对位置判定每颗行星的可见性,这样就把能被观测到的行星计入可见行星中,并且利用这个可见行星的数量进行打分。如果夜空中可以看到的行星越多,那这一天的连珠指数就越大。
其次,我们在意它们是不是呈现近似排成一条线的几何效果。要衡量这一点,最简单的方法是做一个高中学过的最小二乘。通过拟合出来的直线的拟合质量来判断这些行星是不是成一条直线。具体做法是,把同一时刻各行星的黄道坐标点(经度、纬度)输入算法,拟合出一条最佳拟合线,然后看每颗行星到这条线的平均距离或最大距离,距离越小就代表越对齐。但里面有一个小坑是,水星和金星两颗内行星往往跑的特别快,有时候会离黄道特别远。这时候就算其他行星正好排成了一个完美的直线,如果我们把水星金星也放进连珠的判定的话,得出来的分数必然极差。但这其实是不对的,因为这一天还是可以构成一个完美的五星连珠。为了解决这个问题,我们用了一种更稳定的拟合算法叫做RANSAC,它针对水星金星这种例外情况有奇效。
最后,我们往往也会希望行星集中在天球上的某一片区域。因为相比于一条横贯东西的线,如果行星集中在一小片区域形成一条很短的直线,这样的视觉效果就像一支天际弧线上的队伍,会更加震撼。为了描述这一点,我们注意到多数行星的轨道都与黄道面只存在一个小倾角,因此它们的黄道经度是否集中,往往决定了在夜空中看起来是不是扎堆在同一个弧段上。所以我们可以计算当时刻行星经度的分散度(比如极差或标准差),越小就表示它们的分布越紧凑,也就越容易给人几颗行星挤在天际某一带的印象。
有了这三项指标后,我们便能对某一时刻的行星连珠指数做出量化判断。具体步骤是:
- 在指定时间范围(例如2010到2030年)内,每隔一定时间(如每天或更细粒度)计算行星位置。
- 对每个采样时刻,基于这些位置来算出可见行星数量、排列紧密度和经度集中度三项得分。
- 以40%、30%、30%的权重加权合并,得到一个对齐评分。
- 将这一评分随时间作图,就可以看到行星连珠从无到有、再逐渐散去的动态过程。如果哪段时间评分出现显著峰值,极有可能就是一次罕见的n星连珠。
这种方法能让我们从“看起来很整齐”或“好像都在一起”的主观描述,转向相对客观、可重复的数值评估。当评分高的峰值出现时,我们更有把握断言这几天内会出现视觉效果壮观的行星连珠现象。换言之,这套量化思路既可以帮我们回顾过去20年里究竟有哪些时段可能出现n星连珠,也能让我们对未来某年某月行星排队的几率做出相当可靠的预测。而如果我们真的写出程序(开源在https://github.com/grapeot/PlanetAlignment),并且在2010-2030的时间上跑一遍的话,会发现2025年1-2月这段时间并不是特别出彩,在2025年7月会有更符合这个标准的连珠出现。
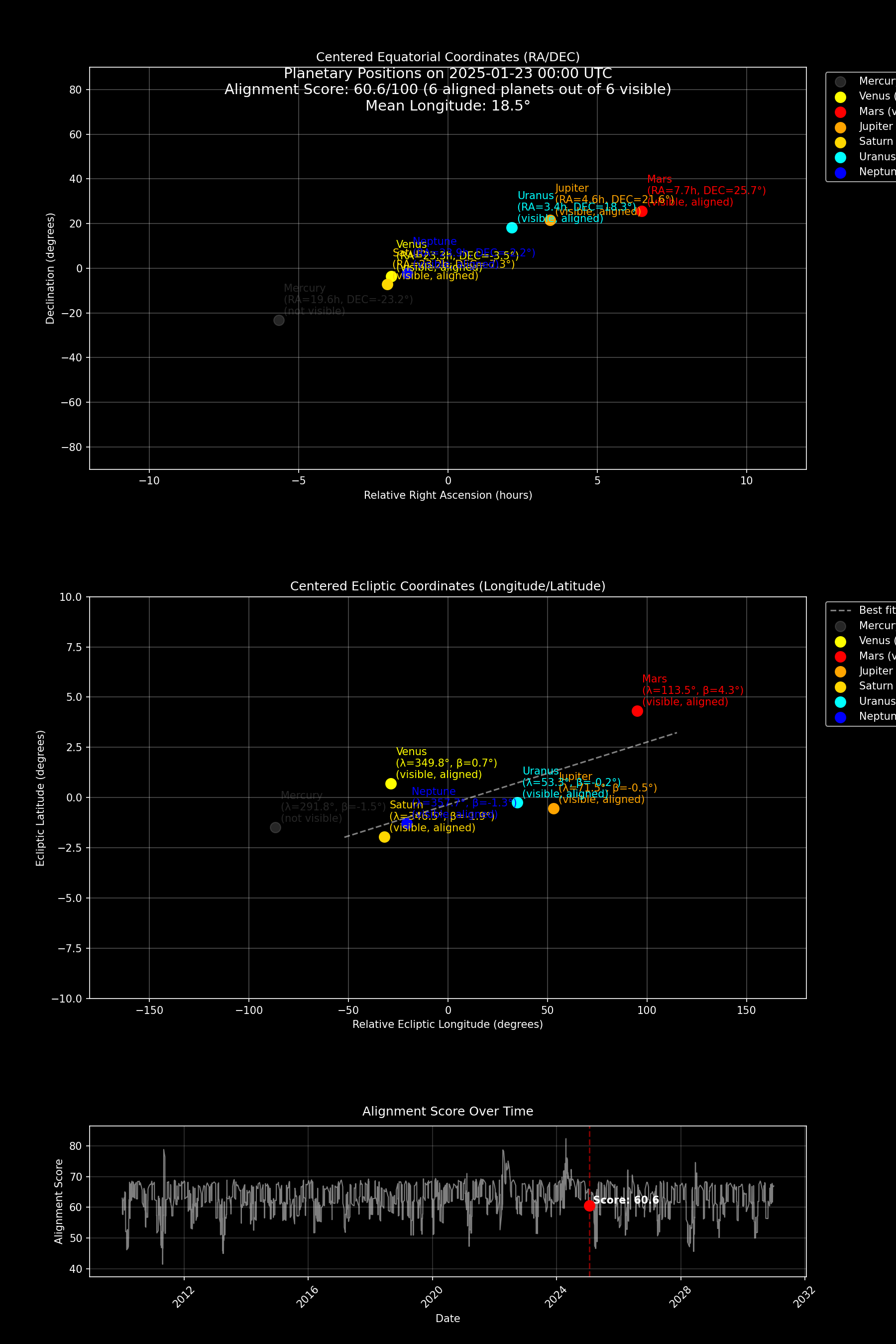
但是要注意的是,虽然我们用了严谨的数学来描述这个现象,整个过程仍然带有相当大的主观性。比如很多其他媒体在讨论九星连珠的时候,并不要求它们聚在天球上的一小块区域。或者,我们这个40%、30%、30%的权重也会极大地影响分数。比如你要是把排列紧密度的权重增加的话,就会发现今年1月、2月的这次连珠分数明显升高。但如果把黄道经度集中度权重升高的话,就会发现它的评分又降低了。这就好像大学排名一样,你把学校的规模的权重升高或者降低,往往会带来大学排名非常剧烈的变动。这么一说,大家是不是就明白了?
所以我想强调,我们要辩证地来看待这篇文章提到的数学思想。一方面,它把一种非常模糊、缥缈的直觉给有效地量化出来,让我们能够在几十年、几百年的尺度里进行快速搜索,用严谨和定量极大提升了我们的效率。但另一方面,在严谨的外表下面,它仍然是一个非常主观的东西。甚至只需要调一些权重,就可以让最终得出的结论发生大幅的变化。所以我们也不能迷信数学。
Comments